A Visualization of Chopsticks
Shortly after graduating from high school, I spent a couple of summers working at various children’s summer camps. There was plenty of downtime in between scheduled activities, and no shortage of simple games that groups of kids and staff could engage in to fill time. Most of these games, like Stella Ella Olla, weren’t all that deep and required little strategy. However, a couple of the games were strangely deep and contained structures inside them that fascinated me intensely at the time. The two games I still think about were called “shotgun” and “chopsticks.” Shotgun is a fascinating mixture of a rhythm game with rock paper scissors; however, I have found no interesting way of visualizing it so a deeper analysis of the game will have to wait for the latter. Chopsticks, on the other hand, is everything I love in a game, it is complicated enough to be interesting, while simple enough to be understandable. As well, it is a folk game, and as such there is no definitive rule set. Different kids played the game slightly differently, but most organically came to agree on the rule set I am using because variations on this rule set generally create less interesting games.
How to play
Both players start facing each other with both hands extended and one finger on each hand extended. The players then take turns adding fingers to their opponent’s hand by tapping their own hand against it. The opponent then gains the number of fingers that they were tapped with. So if I tap your left hand with my left hand that has one finger on it, your left hand gains one finger and extends a second finger accordingly. The opponent may then use their turn to add two fingers to one of my hands. Once a hand has five or more fingers on it, it closes and becomes a fist. Fists cannot be used to tap fingers. However, for my turn, I may give half of the fingers in my remaining hand to open up a fist. This may only be done if the number of fingers on the remaining open hand are even. If it is odd, I cannot split and must tap the opponent’s hand. The winner is the player who manages to close both of their opponent’s hands first. There are variations of the game, sometimes we played the game where hands only closed when the finger count was greater than five (instead of greater than or equal to five). Some kids even tried to make me play versions where splitting is allowed with an odd number of fingers or even when neither fist was closed; however, these games were impossible to end and I stopped playing them.
Analysis
The game is interesting to me for a couple of reasons. The first is that it is a perfect information game that somehow straddles the line between too complicated and too simple. Unlike tictactoe, which can be exhausted after only a few hours of competitive play, chopsticks managed to remained interesting to explore for the entire summer I played it. Yet it is also simple enough that it doesn’t require an advanced chess engines to explore fully. There is also a sense while playing it that something weird is going on with game states, but during my summer exploring it with kids we could never really pin down precisely what that was.
The weirdness of the game stuck with me for several years, and I was determined to visualize it in some way to demonstrate this weirdness. However, conventional tree search algorithms and visualizations failed for a number of reasons. The first and most prominent is that the game does not have a tie condition. Players can return to their initial state, meaning unless someone makes a mistake, the game never ends. This is an issue for tree search algorithms because we can never fully open all the leaves on a node. Most leaves, in fact, can loop back on themselves, creating an infinite recursion loop. Instead, what I had to do was detect when a leaf already exists on the stack, then pretend like that is a tying move. The algorithm would, or course, prefer moves that are winning, but will choose to make a move that can loop in on itself over one that is losing. The program worked something like this. The software begins as a conventional tree search algorithm and opens all the nodes in the tree that it can, stopping whenever doing so would open a node that was already on the stack. In cases where there was a clear winning move, I would record that position as winning. However, in situations where this was not the case, I would store a pointer to all the moves that weren’t losing and therefore looped back in on themselves. Whenever I managed to prove that a new position was winning or losing, I could then return to any position that had a pointer to this position and update it accordingly1. Eventually I would iterate through the tree and no further updates would be left. What remained at this point is a graph of ‘open’ positions that would not result in the opponent winning the game.
Pruning
An important part of the game analysis was pruning the symmetries out of the game, and this game contains a lot of symmetries. Firstly, a players right hand and left hand are symmetric. Having one finger on my left hand is structurally the same as having one finger on my right hand. I solved this by using an internal representation for each hand that assumes the smaller number of fingers is always on the left hand. The number 11 means that it is a player with one finger on both hands, while the number 14 represents a player with one finger on their left hand and four fingers on their right: 41 is an invalid game state as it is a symmetry of 14. The second major symmetry, and the one more difficult to deal with, is player symmetry. Unlike a game like chess, where the black player necessarily has always made one less move than the white player, both players can find themselves in every game state; if the game plays long enough, the game can reset with the opposite player making the first move. This is solvable by picking a representation that is player agnostic. Every time a move is made, the players switch their label. Player one, gets to make a move, then hand the label of player one over to the other player, who makes the next move. In the end the representation I used looks like this: 14-23 - The player to move has one finger and four fingers and is about to make a move against an opponent with two fingers and three fingers. Finally, I removed all the losing moves which change the state representation from a tree, with the opening move at the top, to a cyclical graph.
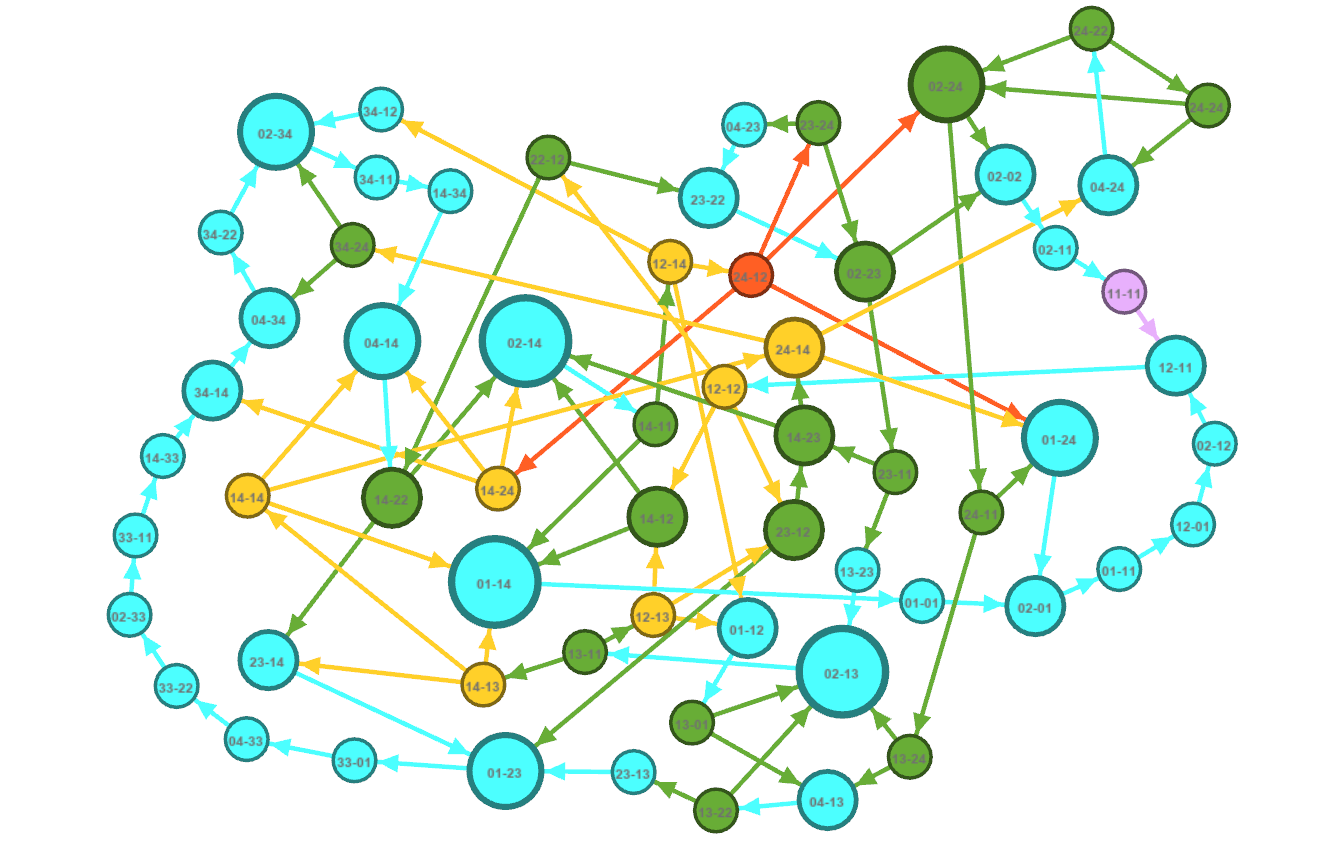
The Visualization
The graph was put together in Gephi, and I added some colorization to demonstrate how much choice a player has. The initial state is purple, blue states only have one non-losing move, green has two, yellow has three, and the single red node has four. Each node is also sized according to how many ways there are to get to it. The biggest nodes have lots of entry points. The purple starting node only points to one state, because when all players have only one finger in all hands their only option is to tap one finger against one other finger. So it is the second player that has to make a choice, but even this choice is forced as tapping their 2 fingered hand on anything will immediately offer the opponent a winning move. The game continues from there.
So about that weirdness I mentioned earlier. Well now I have proof of it. If we take a look on the left side of the graphic, we should notice a chain of 14 consecutive moves starting at 01-23 and ending at 14-22 that all have a forced actions. Any move except the ones listed here offer a winning move to the opponent. Worse, the player that finds themselves at 14-22 can immediately force the players to do the entire sequence again. More skilled players absolutely used this sequence to bully less skilled players during my summer at camp.
I am tremendously proud of this visualization, and I hope that my ramblings have shared just a little bit of the thought that went into it.
-
I learned a ton about how variables work in python by doing this. Honestly, projects like this are one of the main reasons I’m as good at the language as I am. ↩